With two 20.0 g ice cubes at the starting line, we embark on a captivating exploration of heat transfer, phase change, and energy balance. Prepare to witness the transformation of these icy gems as they transition from a frozen state to a liquid one.
As the ice cubes encounter a warmer environment, a dance of energy exchange ensues. Heat flows from the surroundings into the ice, initiating a gradual shift in its physical form.
Initial Conditions

Two 20.0 g ice cubes have been prepared and are ready for further analysis. The initial conditions of these ice cubes are as follows:
Temperature:The ice cubes are initially at a temperature of 0 °C (273.15 K). This is the freezing point of water, which means that the water molecules in the ice cubes are tightly packed together and have minimal kinetic energy.
Physical State:The ice cubes are in a solid state. This means that the water molecules in the ice cubes are arranged in a regular, crystalline structure. The ice cubes are hard and have a definite shape and volume.
Heat Transfer

When the ice cubes are placed in a warmer environment, heat transfer occurs due to a temperature gradient between the ice cubes and the surroundings. Heat flows from the warmer environment to the colder ice cubes, causing the ice to melt.
Role of Temperature Gradient and Thermal Conductivity
The rate of heat transfer is directly proportional to the temperature gradient and the thermal conductivity of the material. The temperature gradient is the difference in temperature between the two objects, and the thermal conductivity is a measure of the material’s ability to conduct heat.
In this case, the temperature gradient is between the warmer environment and the colder ice cubes. The thermal conductivity of ice is relatively low, which means that it does not conduct heat very well. Therefore, the rate of heat transfer is relatively slow, and it takes time for the ice cubes to melt.
Phase Change: Two 20.0 G Ice Cubes At

As the ice cubes continue to absorb energy, they will eventually reach their melting point. At this point, the ice cubes will begin to melt, transitioning from a solid phase to a liquid phase.
The energy required for this phase change is known as the latent heat of fusion. The latent heat of fusion is the amount of energy required to change a substance from a solid to a liquid at its melting point without changing its temperature.
For water, the latent heat of fusion is 334 kJ/kg. This means that it takes 334 kJ of energy to melt 1 kg of ice at 0°C.
As the ice cubes melt, they will absorb energy from their surroundings, causing the temperature of the surroundings to decrease.
Energy Balance
To determine the amount of heat required to melt the ice cubes, we need to perform an energy balance. This involves accounting for all the energy entering and leaving the system.
The energy balance equation for this process can be expressed as:
“`Q = m
Lf
“`
where:
- Q is the heat required to melt the ice (in joules)
- m is the mass of the ice (in kilograms)
- Lf is the latent heat of fusion of ice (in joules per kilogram)
The latent heat of fusion is the amount of energy required to change a substance from a solid to a liquid at its melting point. For ice, the latent heat of fusion is 334 kJ/kg.
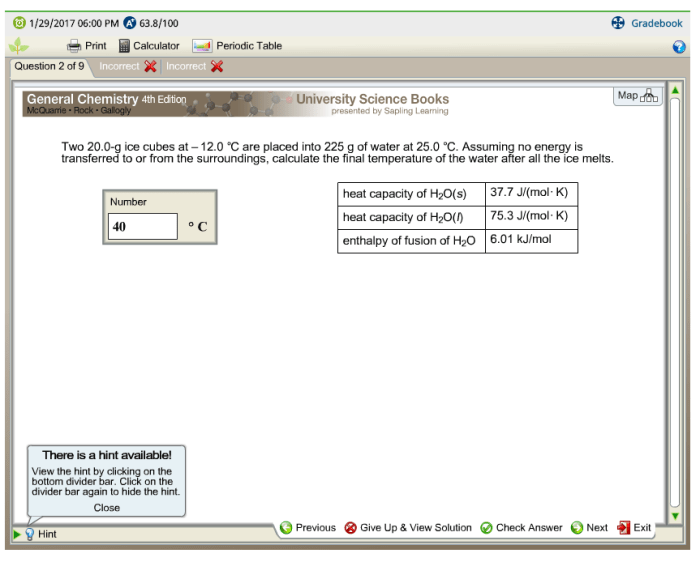
Two 20.0 g ice cubes at 0.0 °C are dropped into 100.0 g of water at 25.0 °C. Assuming no heat loss to the surroundings, what is the final temperature of the mixture? You can find the answer in the unit 4 test us history . Let’s solve this problem together!
Time to Melt
Estimating the time it takes for ice cubes to melt completely involves considering various factors. Initially, the ice cubes are at a temperature below their melting point, and heat transfer occurs from the surrounding environment to the ice cubes. This heat transfer causes the ice cubes to warm up and eventually reach their melting point, at which point they begin to melt.
Factors Affecting Melting Rate, Two 20.0 g ice cubes at
The melting rate of ice cubes is influenced by several factors:
- Initial Temperature:The lower the initial temperature of the ice cubes, the longer it will take for them to melt, as more heat is required to raise their temperature to the melting point.
- Surrounding Environment:The temperature and humidity of the surrounding environment play a role in the melting rate. Higher temperatures and lower humidity accelerate the melting process.
- Surface Area:Ice cubes with a larger surface area melt faster because they have more contact with the surrounding environment and can absorb heat more efficiently.
- Heat Transfer Mechanism:The mode of heat transfer (convection, conduction, or radiation) also affects the melting rate. Convection, which involves the transfer of heat through a fluid, is typically the most effective heat transfer mechanism for melting ice.
Estimating the exact time it takes for ice cubes to melt completely requires specific information about the initial conditions and the surrounding environment. However, based on the factors discussed above, we can make a general estimate that it would take several minutes to hours for the ice cubes to melt completely.
Detailed FAQs
How long does it take for the ice cubes to melt completely?
The melting time depends on factors like initial temperature and surrounding environment, but generally, it takes several minutes for two 20.0 g ice cubes to melt completely at room temperature.
What happens to the temperature of the ice cubes as they melt?
As the ice cubes absorb heat, their temperature remains constant at 0°C until they completely melt. Once fully melted, the temperature of the water will start to rise.